Attention Mechanism

Date: 23.06.22

Writer: 9tailwolf : doryeon514@gm.gist.ac.kr


Introduction

RNN based language model has a chronic problem like Gradient Vanishing. To solve problem, various language model developed(LSTM, GRU, Seq2Seq). But it was impossible to completely eliminate the problem. This is the reason why Attention Mechanism is developed.


Attention

The main idea of attention is literally attention. In attention mechanism, give a high relative word can get high weight to solve gradient vanishing.

1. Similarity

First, We should compare with each word state, that means compare with \(t-1\) hidden decoder state with \(k\) \((1 \leq k \leq N)\) encoder states. Following is a fomular of find similarity. \(e\) is a vector of score, \(s_{k}\) is a hidden decoder state, \(h_{k}\) is a hidden encoder state, \(f\) is a score function.

$$e = (e_{1}, e_{2}, e_{3} ,..., e_{N}), e_{k} = f(s_{t-1},h_{k})$$

There is a various score function. Below is a example of score functions.

  • Content-based Attention \(f(s,h) = \frac{s^{T}h}{|s|\centerdot |h|}\)
  • Additive Attention : \(f(s,h) = V^{T}\tanh{(W_{1}s + W_{2}h)}\)
  • Dot-Product Attention : \(f(s,h) = s^{T}h\)
  • Scaled Dot-product Attention : \(f(s,h) = \frac{s^{T}h}{\sqrt{n}}\)
2. Normalization

To normalize \(e\), we can get weight.

$$\alpha = softmax(e)$$
3. weighted sum

By calculating sum of weight-product, we can get attention value.

$$a = \alpha H = \Sigma_{k=1}^{N}\alpha_{k}h_{k}$$

And Below is a summary of all process.



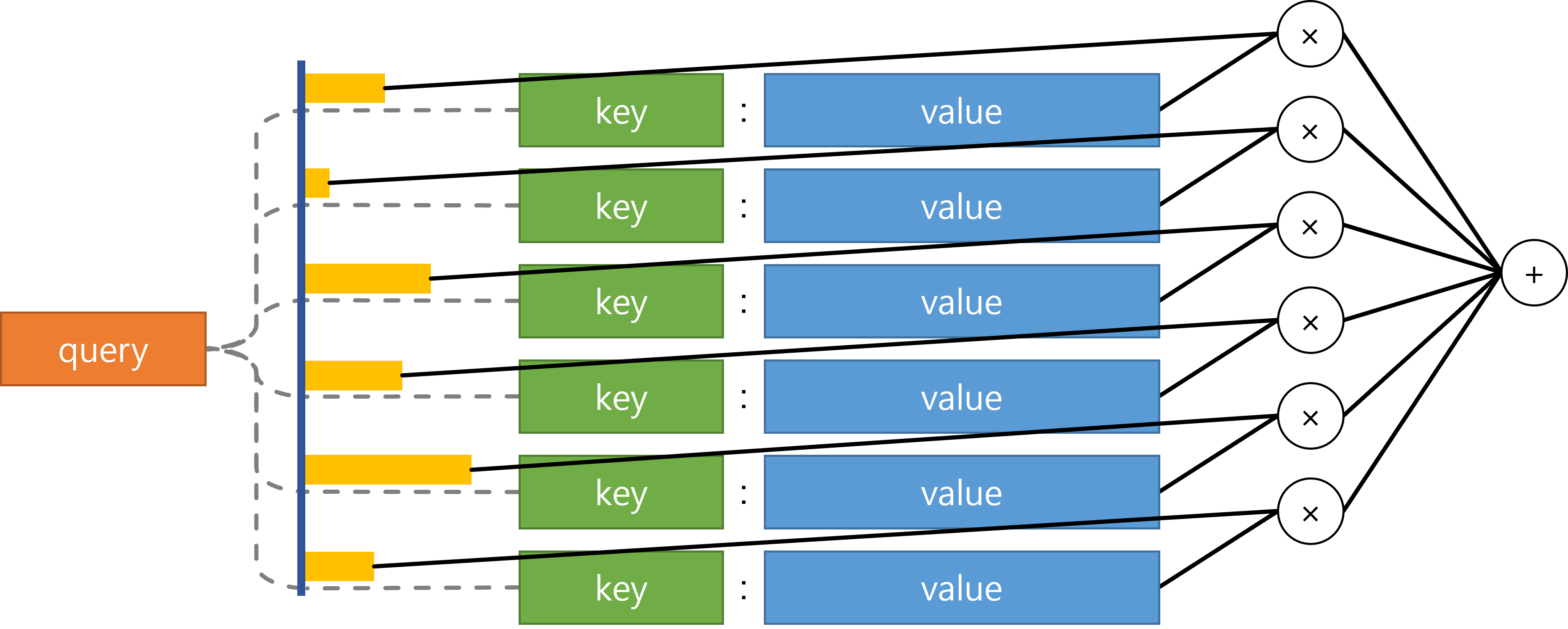
Attention is consist of Query, Key, Value. By making \(A(Q,K,V)\) function to calculate Attention simply. In seq2seq model, Key is same as Value.