Neural Network Language Model

Date: 23.05.11

Writer: 9tailwolf : doryeon514@gm.gist.ac.kr


Introduction

Neural Network Language Model(NNLM) is a new try that can escape rule based algorithm. And the old way in language model, we must consider all vocabulary. For example, when we made sentence consist of 10 words, It needs \(\mid V\mid^{10}\) times of calculation(When \(\mid V\mid\) is \(10,000\), then \(10^{40}\) times of calculation need, Curse of Dimensionality).

Previous Study : Statistical model
$$P(w_{1}^{n}) = \Pi_{i=1}^{n} P(w_{i} \mid w_{1}^{i-1})$$

Above method is a basic statistical language model. To improve calculation, We can apply Markov Chain.

$$P(w_{1}^{n}) = \Pi_{i=1}^{n} P(w_{i} \mid w_{i-1},w_{i-2}...,w_{i-k})$$

Above method is a N-gram language model. By considering k words to estimate word. There is so many way to improve statistical model like smoothing, but it is hard to aviod curse of dimentionality.


Neural Network Language Model

To solve above problem, Neural Network Language Model suggested. In NNLM, there is some conditions.

  1. Every word \(i \in V\) is mapped with vector \(C(i) \in \mathbb{R}^{n}\)
  2. \(C(i)\) is representated the distributed feature vector associated with each word in the vocabulary.
  3. There is a function \(g\) that mapped word matrix \(C(i)\) and probability. And function \(g\) is satisfied below.
$$f(i,w_{t-1},w_{t-2},...,w_{t-n+1}) = g(i,C(w_{t-1}),C(w_{t-2}),...C(w_{t-n+1}))$$

Below is a all process of NNLM.


Process of NNLM


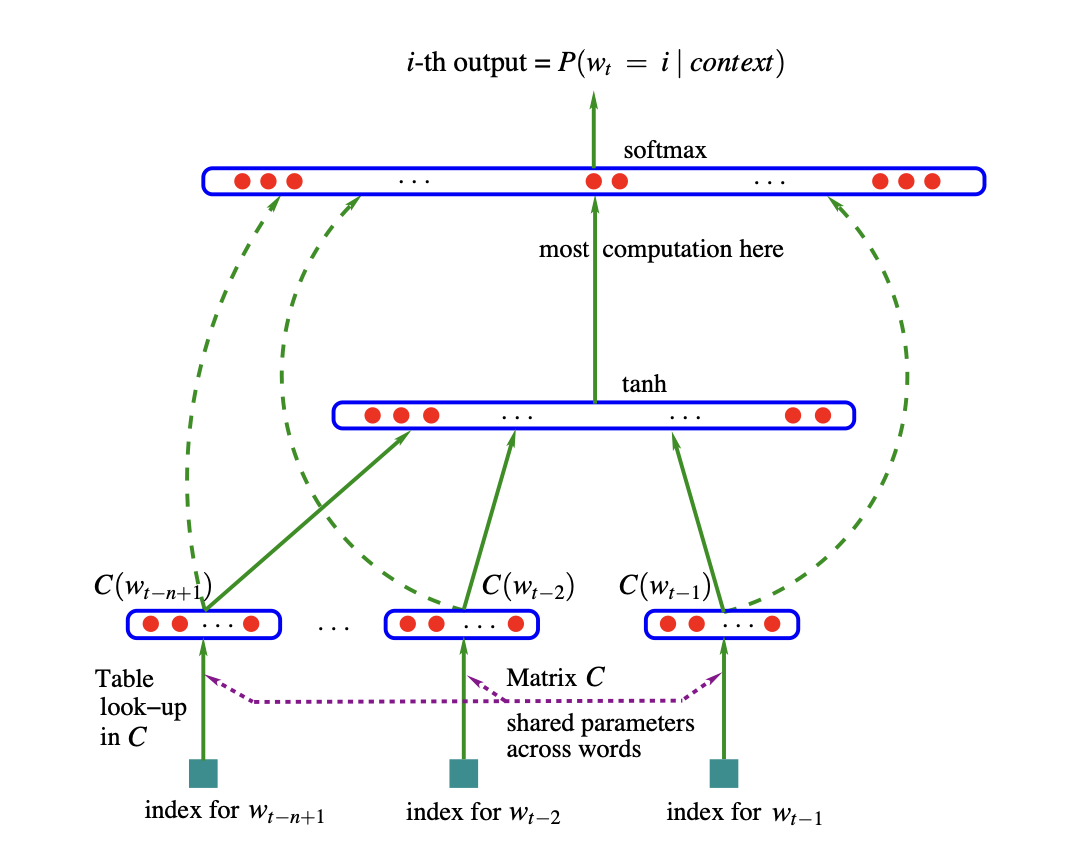
1. Training

In training, we need to find a \(\theta\) that satisfy maximum likelihood function where \(R(\theta)\) is a regularazation term.

$$L = \frac{1}{T} \Sigma_{t} \log f(w_{t},w_{t-1},...,w_{t-n+1};\theta) + R(\theta)$$

By above method, the number of free parameters only scales linearly with \(V\) and only scales linearly with order \(n\).

2. Hidden Layer : First

In NNLM, there is a two hidden layers. First, we use Hyperbolic Tangent function to present probability.

$$f : y = b + Wx + U\tanh(d+Hx)$$

\(b\) is biases with \(\mid V\mid\) elements and d is hidden layer biases with \(h\) elements. \(x\) is a metrix consist of \((C(w_{t-1}),C(w_{t-2}),...,C(w_{t-n+1}))\). \(W\) and \(H\) is a weight. \(W\) is optionally zero.

3. Hidden Layer : Second

In second hidden layer, we use Sigmoid function. But it is not really meaningful.

$$P(w_{t}\mid w_{t-1},w_{t-2},...,w_{t-n+1}) = \frac{e^{y_{w_{t}}}}{\Sigma_{i}e^{y_{w_{i}}}}$$
4. Gradient Ascent

To find \(\theta\) that satisfy maximum likelihood function, we can update the \(\theta\) by below way.

\[\theta' = \theta + \epsilon \frac{\partial \log P(w_{t}|w_{t-1},w_{t-2},...,w_{t-n+1})}{\partial \theta}\]